復習時,要深刻理解考試大綱要求掌握的知識內(nèi)容及相關的考核要求,,從而使得考前復習目標明確,,有的放矢。并將主要知識點進行橫向與縱向的梳理,,分析各知識點之間的關系,,形成知識網(wǎng)絡。
(1)代數(shù)部分:代數(shù)歷來是考試中的重點,,而函數(shù)知識又是代數(shù)部分的重中之重,。要掌握函數(shù)的概念,會求常見函數(shù)的定義域及函數(shù)值,,會用待定系數(shù)法求函數(shù)解析式,,會對函數(shù)的奇偶性和單調性進行判定。函數(shù)的重點是一次函數(shù),、二次函數(shù),、指數(shù)函數(shù)、對數(shù)函數(shù)的圖象和性質,。數(shù)列是代數(shù)部分的又一個重要內(nèi)容,。導數(shù)及其應用是近兩年考試中的一個突出重點,復習的基本策略是注重運算,強調應用,。導數(shù)復習的重點是:①會求多項式函數(shù)幾種常見函數(shù)的導數(shù),。②利用導數(shù)的幾何意義求曲線的切線方程,并能以導數(shù)為工具求函數(shù)的單調區(qū)間,、極值與最大值或最小值,。③解簡單的實際應用問題,求最大值或最小值,。
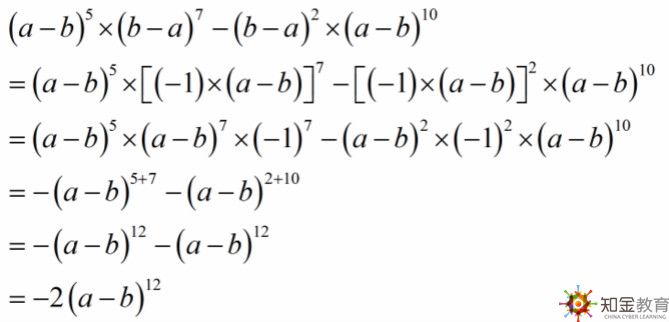
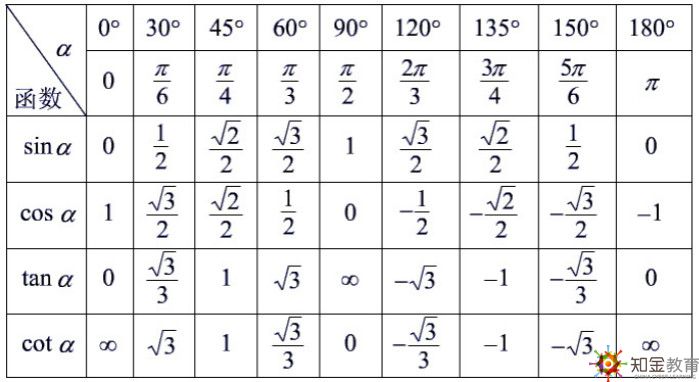
(2)三角部分:在理解三角函數(shù)及有關概念的基礎上,,要掌握三角函數(shù)式的變換,包括同角三角函數(shù)之間的基本關系式,,三角函數(shù)的誘導公式,兩角和兩角差的三角函數(shù)公式,,以及二倍角的正弦,、余弦、正切公式,,并用公式進行計算,、化簡。同時,,要會判斷三角函數(shù)的奇偶性,,會求三角函數(shù)的最小正周期和函數(shù)的單調增減區(qū)間,會求正弦函數(shù),、余弦函數(shù)的最大值和最小值,、值域,尤其要會用正弦定理和余弦定理解三角形,。
(3)平面解析幾何部分:解析幾何是通過坐標系及直線,、圓錐曲線的方程,用代數(shù)的方法研究幾何問題,。平面向量一章,,在理解向量及相關概念的基礎上,要重點掌握向量的運算法則,,向量垂直與平行的充要條件,。直線一章的復習重點是直線的傾斜角和斜率,直線方程的五種形式,,兩直線的位置關系,。要求能根據(jù)已知條件來求直線方程,掌握點到直線的距離公式,。圓錐曲線一章的復習重點是圓的標準方程和一般方程,,直線與圓的位置關系,橢圓、雙曲線以及拋物線的標準方程,、圖形及性質,,特別要注意直線與圓錐曲線的位置關系。